18 February, 2006
1. Introduction
2. Theory
2.1. Time derivative discretization
2.2. 3-point difference formulas for the spatial domain
2.3. "Mass-balance" difference formulas
2.4. Algorithm to solve the resulting algebraic equations
3. Vectorized algebraic-equations solver for TRANSIENT (NL3BANDV)
3.1. Optional constraints (concentration bounds)
4. Conditions for terminating the iteration process in NL3BANDV
5. How to install and use TRANSIENT
5.1. Installation
5.2. Writing your own Problem Definition Module
5.3. Running TRANSIENT-based programs
6. Overview of TRANSIENT
6.1. Pseudocode for the TRANSIENT main function
6.2. Adaptive time-stepping algorithm
6.3. Precision control
6.4. Exit codes
7. The details of writing your own PDM
7.1. Header file with PDM-dependent input parameters
7.2. Source code for the user supplied functions
8. Demonstration examples
8.1 Demo 1. Uniform corrosion
8.2 Demo 2. Gas generation and diffusion
8.3 Demo 3. Stochastic surface growth
8.4 Demo 4. Brusselator
References
Appendix: TRANSIENT V4.3-beta "packing list"
Although it is often sufficient to know only the steady state of chemical systems, their time evolution (transient behavior) can be of interest, too. For example, when the transition into a steady state is very slow, or when the transient behavior itself is of the main interest, such as in corrosion or when a system oscillates about an unstable steady state. In such cases, numerical solution of the underlying reaction-diffusion equations is desirable. This solution can be conveniently obtained by finite difference methods. In this approach, all partial derivatives are replaced by suitable finite differences, and to propagate the solution in time, the resulting nonlinear algebraic equations are repeatedly solved numerically.
Spotnitz [1] introduced in 1994 a C package called NL3BAND implementing Newman's method [2-5] for solving banded nonlinear algebraic systems of equations, specifically those originating from electrochemical steady state problems. Newman's method is based on banded matrices and the Newton-Raphson (NR) method for solving systems of nonlinear equations.
Here I adopt this approach to the solution of arbitrary systems of coupled, nonlinear, parabolic partial differential equations in two independent variables (time and one spatial variable), and present a C package called TRANSIENT that can be easily applied to a large variety of such problems. TRANSIENT uses a general implicit differencing scheme for the time domain.
A list of all problem-independent modules constituting the TRANSIENT engine (solver) together with their brief descriptions is in the Appendix. The main (control) module of this package, transien.c, is based on an heuristic adaptive time-stepping algorithm that repeatedly invokes a vectorized version of NL3BAND (NL3BANDV), in which all matrices are treated as linear one-dimensional arrays. In this scheme, the magnitude of the next time step is determined also (or exclusively) by the number of NR iterations of the NL3BANDV solver.
For a given system of differential equations to be solved, the user must supply a problem definition (or description) module (PDM) consisting of the list of model input parameters (placed in a separate C header file) and a number of C functions (placed in one or possibly more C source files). Demonstration examples of such modules, demo1 to demo4 are supplied in subdirectories demo/demo1 to demo/demo4 of the TRANSIENT distribution package. These examples can serve as easy-to-follow templates for your own problems. Example No. 2 (demo2) also includes some TRANSIENT validation: it demonstrates a high degree of agreement of TRANSIENT's results with an analytical solution for this example. Example No. 1 (demo1) deals with a slow corrosion process reaching its steady state at about 4×108 a (years). Simulation of such processes with reasonable accuracy in relatively short CPU time seems to be the strength of TRANSIENT.
The purpose of TRANSIENT is to solve a set of n coupled partial differential equations of the parabolic type, e.g., of the form
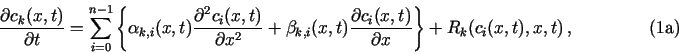

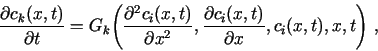
Additional constraints on ck may be set as described in Sec. 3.1.
To obtain numerical solution of eqs. (1), both x and t have to be discretized: there are N, generally nonequidistant, grid points xj; j = 0,..., N - 1, and an a priori unspecified number of time instants tl; l = 0, 1,.... Values of ck(x, t) will be calculated only at these discrete values of x and t; and ck(xj, tl) often abbreviated to ck(j, l ).
It is assumed that ![]() ,
, ![]() and Rk
in eq. (1a) are continuous functions of x and t, except perhaps at
a small set of discrete values of x. Such discontinuities
must be treated with care: for the highest accuracy use a spatial
grid in which the position of each discontinuity coincides with
a grid node, and use a consistent discretization.
This will be discussed to some extent
in Sec. 2.3 and also in
Secs. 8.1 and 8.2 (demonstration examples demo1 and demo2).
and Rk
in eq. (1a) are continuous functions of x and t, except perhaps at
a small set of discrete values of x. Such discontinuities
must be treated with care: for the highest accuracy use a spatial
grid in which the position of each discontinuity coincides with
a grid node, and use a consistent discretization.
This will be discussed to some extent
in Sec. 2.3 and also in
Secs. 8.1 and 8.2 (demonstration examples demo1 and demo2).
All the derivatives in eq. (1) must be replaced by suitable difference formulas. This discretization is the responsibility of the PDM author. TRANSIENT is an open platform for the numerical solution of systems of eqs. (1), and must be provided with their discretized form. Difference formulas listed below represent some obvious choices. Most of them were used in the demonstration examples. My experience shows, that for the spatial domain, the mass-balance approach of Sec. 2.3 gives the best results.
2.1. Time derivative discretization
For the time derivative at the j-th grid point, one can always use
![]()
2.2. 3-point difference formulas for the spatial domain
On the right-hand side of eq. (1a) the standard approach at points
at which the discretized functions are continuous is to use the usual
3-point central difference formulas for the given type of grid in a
differencing scheme of general
implicitness 1 - ![]() , 0
, 0![]()
![]()
![]() 1, mixing together the "old" solution
at tl with the "new" (to be computed) solution at tl+1:
1, mixing together the "old" solution
at tl with the "new" (to be computed) solution at tl+1:
![]() is the fraction of the old solution in this mixture.
Let us introduce
is the fraction of the old solution in this mixture.
Let us introduce
![]()
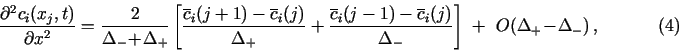
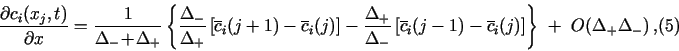
In evalf() of the demonstration PDM's 1, 2 and 4,
![]() (j)
(j) ![]() cBar0[i],
cBar0[i],
![]() (j - 1)
(j - 1) ![]() cBarM[i]
and
cBarM[i]
and ![]() (j + 1)
(j + 1) ![]() cBarP[i],
in demo3.c it is hBar0, hBarM and hBarP.
cBarP[i],
in demo3.c it is hBar0, hBarM and hBarP.
Note that ![]() (j) as defined in eq. (3) correspond to
ck(xj, t
(j) as defined in eq. (3) correspond to
ck(xj, t![]() ) at
t
) at
t![]() = tl + (1 -
= tl + (1 - ![]() )(tl+1 - tl) =
)(tl+1 - tl) = ![]() tl + (1 -
tl + (1 - ![]() )tl+1
as calculated by linear interpolation between
ck(j, l ) and ck(j, l + 1). Thus the last term in eq. (1a) should
in this differencing scheme be replaced by
Rk(
)tl+1
as calculated by linear interpolation between
ck(j, l ) and ck(j, l + 1). Thus the last term in eq. (1a) should
in this differencing scheme be replaced by
Rk(![]() (j), xj, t
(j), xj, t![]() ).
Similarly, if
).
Similarly, if ![]() and
and ![]() depend explicitly on time,
they should also be evaluated at t
depend explicitly on time,
they should also be evaluated at t![]() in the finite difference
replacement of eq. (1a). In terms of variables exported from TRANSIENT
into a PDM, t
in the finite difference
replacement of eq. (1a). In terms of variables exported from TRANSIENT
into a PDM, t![]() = t - Tau / tStepInv. In demo1.c,
t
= t - Tau / tStepInv. In demo1.c,
t![]() is stored in the variable tMean.
is stored in the variable tMean.
Usually, the best choice for ![]() should be
should be ![]() = 0.5, corresponding
to t
= 0.5, corresponding
to t![]() = (tl + tl+1)/2.
Note that only in this case the error of the difference formula
in eq. (2) is of the
second order in the time step, otherwise it is of the first order in time step.
= (tl + tl+1)/2.
Note that only in this case the error of the difference formula
in eq. (2) is of the
second order in the time step, otherwise it is of the first order in time step.
![]() = 0.5 gives the Crank-Nicolson scheme, which for equidistant grids is
of the second order both in space and time, and for pure diffusion is stable
for arbitrary time-step size. It is expected to be stable for large time
steps also for many types of the reaction term Rk(ci(x, t), x, t).
= 0.5 gives the Crank-Nicolson scheme, which for equidistant grids is
of the second order both in space and time, and for pure diffusion is stable
for arbitrary time-step size. It is expected to be stable for large time
steps also for many types of the reaction term Rk(ci(x, t), x, t).
![]() = 1 gives the fully explicit scheme which is stable only for very
small time steps, and
= 1 gives the fully explicit scheme which is stable only for very
small time steps, and ![]() = 0 gives a fully implicit scheme stable for
arbitrary time steps. Thus, at first always use
= 0 gives a fully implicit scheme stable for
arbitrary time steps. Thus, at first always use ![]() = 0.5, if there are any
problems, try
= 0.5, if there are any
problems, try ![]() < 0.5.
< 0.5.
The boundary conditions in eq. (1b) do not contain any time derivatives,
and so they could always be discretized directly at t = tl+1. Thus, in
![]() k, left the following 3-point forward difference
formula could be used at j = 0:
k, left the following 3-point forward difference
formula could be used at j = 0:
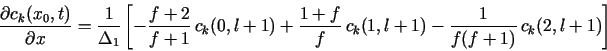
![]()
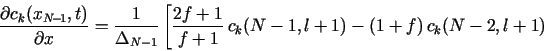
2.3. "Mass-balance" difference formulas
When ![]() and
and ![]() are independent of x,
using difference formulas (4) and (5) is equivalent to integrating
eq. (1a) with respect to x (at t = t
are independent of x,
using difference formulas (4) and (5) is equivalent to integrating
eq. (1a) with respect to x (at t = t![]() )
between two neighbouring grid midpoints xj -
)
between two neighbouring grid midpoints xj - ![]() /2
and xj +
/2
and xj + ![]() /2, and then using the obvious 2-point difference
formulas for the first derivatives and for the function values at the
midpoints, i.e.
/2, and then using the obvious 2-point difference
formulas for the first derivatives and for the function values at the
midpoints, i.e.
![]()
![]()
![]()
To obtain a consistent discretization throughout the model, it is
desirable to extend this integrational or "mass-balance" approach to all
the grid nodes, including the model end-points and the nodes with
discontinuities. For the model end-points, the integration is done from
xleft to xleft + ![]() /2 (or from
xright -
/2 (or from
xright - ![]() /2 to xright).
One will still use eqs. of type (7) at the first (or last) grid midpoint.
But at xleft (or xright) one will use the solution of
eqs. (1b) for the unknowns
/2 to xright).
One will still use eqs. of type (7) at the first (or last) grid midpoint.
But at xleft (or xright) one will use the solution of
eqs. (1b) for the unknowns ![]() (xb, t) obtained
in terms of ci(xb, t) and possibly t. For example, for the trivial
case of von Neumann b.c.,
(xb, t) obtained
in terms of ci(xb, t) and possibly t. For example, for the trivial
case of von Neumann b.c.,
![]()
![]() =
= ![]() , this
solution is simply equal to Const. In case of nonlinear form of
eq. (1b), one has to solve it numerically at the beginning of each
NL3BANDV (see Sec. 2.4 and Sec. 3) iteration.
This process will be discussed in more detail in Sec. 8.1
(e.g., eq. (32)).
, this
solution is simply equal to Const. In case of nonlinear form of
eq. (1b), one has to solve it numerically at the beginning of each
NL3BANDV (see Sec. 2.4 and Sec. 3) iteration.
This process will be discussed in more detail in Sec. 8.1
(e.g., eq. (32)).
For the inter-media interfaces, i.e., at grid nodes with discontinuities
in ![]() ,
, ![]() and R in the interior of (xleft, xright),
the integration of eq. (1a) in the vicinity of such a grid point must be
performed separately in (xj -
and R in the interior of (xleft, xright),
the integration of eq. (1a) in the vicinity of such a grid point must be
performed separately in (xj - ![]() /2, xj) and in (xj, xj +
/2, xj) and in (xj, xj + ![]() /2).
At both outer ends of this interval, one can still use eqs. (7).
At xj then the discontinuity relations between ck (or
/2).
At both outer ends of this interval, one can still use eqs. (7).
At xj then the discontinuity relations between ck (or
![]() ck/
ck/![]() x) on two sides of xj (resulting e.g. from the
continuity of the diffusion flux at xj). More details can be found
in the demonstration examples of Secs. 8.1 (e.g., eq. (31)),
8.2 and 8.4.
x) on two sides of xj (resulting e.g. from the
continuity of the diffusion flux at xj). More details can be found
in the demonstration examples of Secs. 8.1 (e.g., eq. (31)),
8.2 and 8.4.
This approach is called "mass-balance" discretization because it divides the whole model into "integration" elements extending from one grid midpoint to the neighbouring one (or to the end-point of the model). It conserves mass locally everywhere by accounting for the mass fluxes crossing the boundaries between these elements or through the model faces. It is actually a convection-less equivalent of the Nodal Point Integration method of Runchal [6] used for two- and three-dimensional spatial domains. Runchal [6] also reports that his method gives high precision results. It is a simpler relative of the finite element method (or a hybrid between the finite element and finite difference methods).
2.4. Algorithm to solve the resulting algebraic equations
Upon discretizing eqs. (1) as described above, we get a system of n×N equations of the form
![]()
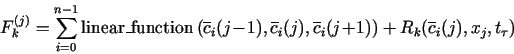
![]()
The set of, possibly nonlinear, algebraic equations (8a) is solved by the
NR method of ref. [1]. In this approach, Fk(j) are
expanded about some trial point,
indicated by ![]() , and only linear terms of the Taylor series
expansion are kept: e.g., Fk(j)(ci(m, l + 1), ci(m, l )) is, for
1
, and only linear terms of the Taylor series
expansion are kept: e.g., Fk(j)(ci(m, l + 1), ci(m, l )) is, for
1![]() j
j![]() N - 2, approximated by
N - 2, approximated by
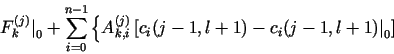
![]()



Do not forget the factor
1 - ![]() =
= ![]()
![]() (j)/
(j)/![]() ck(j, l + 1) (denoted New
in the demonstration PDM's) in the contributions to the Jacobian submatrices
(10), (11) and (12) for j = 1 to N - 2 from the first two terms
(generalized diffusion term
and the reaction term Rk) of Fk(j) in eq. (8b).
ck(j, l + 1) (denoted New
in the demonstration PDM's) in the contributions to the Jacobian submatrices
(10), (11) and (12) for j = 1 to N - 2 from the first two terms
(generalized diffusion term
and the reaction term Rk) of Fk(j) in eq. (8b).
Because 3-point difference formulas (6) may be used at the end-points, the
equivalents of truncated expansion (9) for j = 0 and N - 1 contain two more
matrices with possibly nonzero elements:
![]() with components
with components


Substituting all these truncated expansions for Fk(j) into eq. (8a), one gets a linearized set of equations that in matrix form reads
![]()
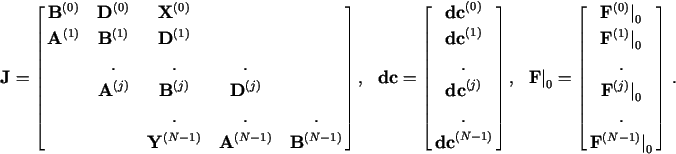
The solution strategy is to evaluate ![]() and
and ![]()
![]() at some
at some ![]()
![]() =
= ![]() , and solve eq. (15)
for
, and solve eq. (15)
for ![]() . If the absolute value of
. If the absolute value of ![]() (and preferably also
(and preferably also
![]()
![]() ) approaches zero, the vector
) approaches zero, the vector
![]() =
= ![]() +
+ ![]()
![]() is accepted as the
solution. Else
is accepted as the
solution. Else ![]() is used as the new trial point
is used as the new trial point
![]()
![]() and the process is repeated until convergence is obtained,
or signs of divergence or oscillations are detected.
In our case, the most suitable initial guess for the unknown
ck(j, l + 1) is obtained by linear extrapolation
of ck(j, l - 1) and ck(j, l ) to the next time instant tl+1.
and the process is repeated until convergence is obtained,
or signs of divergence or oscillations are detected.
In our case, the most suitable initial guess for the unknown
ck(j, l + 1) is obtained by linear extrapolation
of ck(j, l - 1) and ck(j, l ) to the next time instant tl+1.
In order to solve eq. (15), a memory-use-minimizing modification of the procedure of ref. [1] is used: First the upper-lower decomposition of J is done to get
![]()
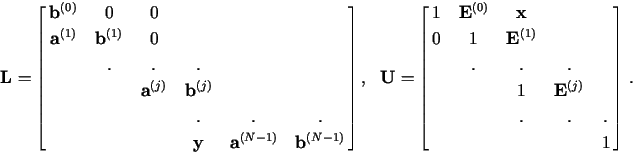
![]()
![]()
The algorithm is as follows:
for j = 0 do:
| |
|||
| |
for j from 1 to N - 2 do:
| |
|||
| |
|||
| if (j = 1) { |
|||
| |
|||
| |
for j = N - 1 do:
| |
|||
| |
|||
| |
|||
| |
|||
| |
In the end, the back substitution of eq. (17) is used to solve for the
- ![]() , which will again be stored in
, which will again be stored in ![]() (j):
(j):
| for j from N - 2 to 1 by -1 do: | |
|||
| for j = 0 do: | ||||
| |
3. Vectorized algebraic-equations solver for TRANSIENT
(NL3BANDV)
In the TRANSIENT code, the number of equations n is stored in the variable neqns, and the number of nodes N is in nnodes in the file transien.c and in NJ in nl3bandX.c (X stands for v or 1).
The algorithm described in Sec. 2.4 is implemented in the function
runband() in file nl3bandv.c. For matrix inversion and LU
decomposition, modules matinvv.c and lufacv.c are further needed.
A simplified version of nl3bandv.c for ![]() = 1 is in the
file nl3band1.c. This version does not need any other modules,
and is almost two times faster than nl3bandv.c called with
= 1 is in the
file nl3band1.c. This version does not need any other modules,
and is almost two times faster than nl3bandv.c called with ![]() = 1
(compare e.g. the speed of demo2a and demo2av of the standard demonstration
set; see Sec. 5.1.). The names and arguments of functions
defined in nl3bandv.c and nl3band1.c are identical.
= 1
(compare e.g. the speed of demo2a and demo2av of the standard demonstration
set; see Sec. 5.1.). The names and arguments of functions
defined in nl3bandv.c and nl3band1.c are identical.
nl3bandX.c repeatedly invoke evalf() to calculate
![]()
![]() and matrices (10) through (14) for one j at
a time. evalf() must be supplied by the user as part of a PDM.
and matrices (10) through (14) for one j at
a time. evalf() must be supplied by the user as part of a PDM.
Because the dimensions (n and N) of the various two- (three-)dimensional arrays involved will vary from problem to problem, these arrays are allocated memory dynamically. To be able to refer to them in all modules as to multi-dimensional arrays, they would have to be declared as pointers to array of pointers (to array of pointers). This would consume some memory and may slow down the execution because of a series of pointer evaluations for each matrix element. This was not an issue when a single set of equations was solved per problem in the original steady-state-only NL3BAND of ref. [1]. TRANSIENT may handle hundreds of thousands of time steps in a single run, i.e., hundreds of thousands of runband() invocations. Then any savings in CPU time may be important. Therefore, TRANSIENT uses a "vectorized" version of NL3BAND, NL3BANDV, that stores all multi-dimensional arrays as linear vectors ("row by row", i.e., the last subscript varies the fastest). These vectorized modules have file names that end with a "v" ( ... v.c).
In a PDM (see section 5), the number of equations (row dimension of all
matrices involved) can always be declared a constant, e.g.,
#define NEQNS
neqns
Then one can define a new type - vector of length NEQNS, e.g.,
typedef double ROW[NEQNS]
and treat all the two-dimensional
matrices as pointers to ROW (see demo1.c and demo4.c).
Thus, when writing a PDM, one can still enjoy the convenience
of the normal matrix notation when dealing with concentrations or
the Jacobian submatrices (10) to (14),
and at the same time save some memory and especially the CPU time.
To this end, the order of matrix elements in TRANSIENT's dynamical vectorized
storage of matrices is the same as in matrices declared with fixed numbers
of elements. Just apply the type cast operator when passing pointers to
matrices between transien.c and a PDM:
(ROW*)
when passing a pointer from TRANSIENT to a PDM, and
(double*)
in the other direction.
3.1. Optional constraints (concentration bounds)
Bounds on the range of each dependent variable (concentration) may be set up to be enforced in runband after each iteration. This is done with the help of bound definition arrays (BDA) described below. The addresses of two arrays of pointers *LB[NEQNS] and *UB[NEQNS] must be supplied from a PDM through the arguments ***LBp and ***UBp of the function initNL3BANDV(). LB[k] points to a BDA that defines the lower bound for the k-th dependent variable. Similarly, UB[k] points to a BDA that defines the upper bound for the same variable. If the bounds for several different variables are the same, only one BDA needs to be set up for all of them, with all the respective LB or UB pointers pointed to it. If there is no upper or lower bound in effect for the k-th concentration, UB[k] or LB[k] may be set to NULL. Similarly, if nothing is assigned to **UBp or **LBp (predefined to NULL), no upper or lower bounds are set for all dependent variables. More details are at the beginning of nl3bandv.c.
Individual bounds for the k-th dependent variable may be changed during a transient calculation by calling the function changeBound(int k, char which, double *BDA), where which is either 'l' or 'u' for the lower or upper bound, respectively, and BDA points to the new (modified) bound definition array.
BDA are designed so as to minimize the memory and CPU time requirements for the
bound checking. Four types of bounds are recognized, distinguished
by the value of the 0-th element of a BDA:
0 - no bound is defined (no further BDA elements are required);
this is equivalent to setting UB[k] or LB[k] to NULL;
1 - a constant bound (which is equal to the next, i.e., the 1st,
BDA element) applies for all nodes;
2 - defines a piece-wise constant bound (an arbitrary even number of BDA
elements must follow, each couple consisting of a bound value followed by the
index of the last node for which this bound holds; the last couple is
recognized by the value of its node index which must be either
smaller than the
previous node index (e.g. equal to 0), or be ![]() N - 1);
N - 1);
3 - sets a different bound for each node (must be followed
by N values of bounds for nodes 0 through N - 1).
4 - can be used for lower bound only to suppress the numerical noise;
sets the same zero cutoff Zc for
all nodes; Zc is equal to the next (1st) BDA element.
Usage: if ci < Zc, ci is set exactly to 0.
The function startband() checks whether the bounds are defined consistently - whether, if both defined for the same k, the lower bounds are less than or equal to the corresponding upper bounds at all nodes.
4. Conditions for terminating the iteration process in
NL3BANDV
TRANSIENT V3.11 is designed to minimize the number of situations when a transient solution run would fail to complete (i.e., fail to reach an arbitrary final time tEnd). The run is not being terminated if a certain predetermined level of NR precision cannot be achieved. It reports to the user the achieved precision as indicated by the quantities cresidT through fresidM defined below. This is done periodically in the headers of the profiles output files, and with monitor=2 also continually on the screen.
Currently only the following value is used in the convergence criteria of the NR iterative algorithm described in section 2:
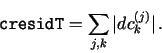
![]()
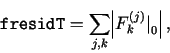
![]()
Basically, NR algorithm continues as long as cresidT decreases significantly with respect to its value in the first NR iteration averaged over time from the beginning of the run. The degree of this decrease can also controlled by the the control input parameter Prec (precision). The default value of Prec=0 corresponds to a decrease by a factor of 10-4 (if achievable), a general value to a decrease by 10-(4+Prec) (the larger Prec, the better convergence is required; small negative values of Prec are allowed and give smaller than default precision, positive Prec larger than default precision). It is expected that the degree of convergence defined by Prec is achieved within nIter NR iterations. TRANSIENT is trying to adjust the magnitude of the time step to the value of nIter. For the details of these convergence conditions see the file nl3_conv.h (which can be easily customized by the user if necessary), and also the line converting the value of the variable Prec in nl3bandX.c itself.
The "concentration" bounds are enforced immediately after each NR iteration only if the macro NR_BOUNDS is set to 1 (see defs.h).
5. How to install and use TRANSIENT
Create an empty directory on your hard disk that will serve as the TRANSIENT root directory. Let us call it TRD (in what follows, all the directory and file names will be given relatively to TRD, unless they explicitly contain TRD; except that sometimes no path is given when it is absolutely obvious. If you got TRANSIENT on a CD, just copy the contents of the CD into TRD.
The preferred way is to get TRANSIENT from the Web.
Download transientVx.xx.tgz (not available right now, sorry),
and unpack this archive into the TRD:
demo\demoX\DEMOX makefiles; on VMS, use MAKEDEMOS.COM.)
The exact configuration of TRANSIENT (inclusion of various optional features) is controlled by the current state of the file defs.h, which can be edited to suit a particular PDM before the compilation and linking of the TRANSIENT modules with a PDM. The settings in this file are fully respected by the Unix and MS makefiles residing in the individual demo/demoX directories.
However, when the standard set of demonstration programs (for the four demonstration PDM supplied with TRANSIENT) is made by the Unix or Visual C++ makefiles in TRD or by the VMS MAKEDEMOS.COM command procedure, the current state of defs.h is overridden by the compiler command line flags (defs.h is written so that command line flags have precedence). The standard set represents a selection of possible TRANSIENT configurations as used with the sample PDM supplied with TRANSIENT. Although the standard set is made without changing the state of defs.h, it represents partly what can be set in defs.h.
The standard set will appear in directory demo/bin, and consists of these seven programs:
5.2. Writing your own Problem Definition Module
To use TRANSIENT for their own problems, the user must prepare a PDM consisting
of a C header file containing the list of all the model parameters, and of
one or more C source files with the code for the following functions:
int get_neqns_etc(void)
void generate_grid(void)
void Initialize(double *cp, double *c_op)
void initNL3BANDV(double***LBp, double***UBp, double*F, double*A, double*B, double*D)
void auxiliary_parameters_for_evalf(void)
void evalf(int j)
void pr_profiles(int MaxIter)
void read_profiles(char *filename)
void init_Other(void)
int update_Other(void)
void pr_Other(int only_Other)
More details will be given in Sec. 7. Use the source, header and make files from the individual demo directories as templates for writing and maintaining your own projects (PDM). After compilation, link the PDM together with the modules that constitute TRANSIENT, contained in TRD.
5.3. Running TRANSIENT-based programs
All the input and output is handled by the TRANSIENT engine, and is thus essentially the same for all PDM. Let us use demo1 to illustrate how to run any TRANSIENT-based code. Only the first three lines below are demo1 specific. For other PDM, they would be replaced by the title specified in get_neqns_etc() (see Sec. 7), or by the string "Unnamed PDM". Also, any occurrence of 'demo1' on the second help page would be replaced by the name of the respective executable.
Typing just demo1 without any command-line options (may have to be
preceded by its path, such as ..../TRD/demo/bin/demo1) will produce
this help page:
TRANSIENT
Demonstration No. 1
Uniform Corrosion and Transport of Corrosion Products
.----- p o w e r e d b y -----.
| TRANSIENT V3.01 nonlin parabolic diff equation solver |
`----- http://transient.mkolar.org/ -----'
To get help on how to run this program, enter: ???
If you continue now, default output files _T_*, par_T_, diag_T_ and
stat_T_ will be created.
If you end input now, default input parameter values would be used.
You can first modify any input parameters in arbitrary order, one at
a time, by entering the name of an input parameter followed by its
new value, separated from the name by spaces or/and an equal sign.
A missing value is interpreted as a zero number, empty character or string).
To end input (start calculation), enter end or press Ctrl+D .
At any time during this input phase, you can also enter:
?c- to list the current values of all control parameters;
??c- to also get extensive help on the role of each control parameter;
?m- to list the current values of all model parameters;
??m- to also get any available help on model parameters;
?<str> to list the current values of all input parameters whose
names start with <str>; e.g. ?tSt;
??<str> to also get available help for input parameters starting with <str>;
? to reprint this interactive menu;
ex[it] to terminate execution;
qu[it] - " -
by[e] - " -
Ctrl+C will terminate execution at any stage.
This was produced in Linux. In MS Windows or VMS, Ctrl+D would be
replaced by Ctrl+Z.
Entering now '???' will produce:
TRANSIENT
Demonstration No. 1
Uniform Corrosion and Transport of Corrosion Products
.----- p o w e r e d b y -----.
| TRANSIENT V3.01 nonlin parabolic diff equation solver |
`----- http://transient.mkolar.org/ -----'
Usage:
To get help: demo1 -h ... prints this page
demo1 -d ... lists all input parameters and
their default values
demo1 -p ... as -d plus any available info on parameters
demo1 -c ... lists only control parameters,
their purpose and default values
To run: demo1 ['Output' [[<] 'Input']]
'Output' ... "root" of names of output files: if SepProf=0,
there is a single file 'Output' for (concentration) profiles;
otherwise profiles for I-th output time are written into 'Output'I;
Input parameters and all the optional output generated by
init_Other, update_Other and pr_Other are written into a
file whose name is created by adding prefix "par" to 'Output'.
Diagnostic output (minima and maxima of tStep, cDiffM, and
all iter between pr_Other times, or at most over 1000 time
steps) is written into a file with prefix "diag" added to 'Output'.
CPU times and more are written into a file with prefix "stat".
'Input' ... name of the input file; only some or none input
parameters need be read in, defaults are used for the rest.
Default files: 'Input': `stdin`
'Output': _T_*
par'Output': par_T_
diag'Output': diag_T_
stat'Output': stat_T_
and the execution will terminate. This second help screen is identical with what one gets after typing demo1 -h .
For example, to run TRANSIENT (demo1) with the default values of input parameters, or to change some of the input parameters interactively at the beginning of the run, and store the results in files parD1o, diagD1o, statD1o and D1o (or D1o1, D1o2, ..., depending on the final value of the input parameter sepProf), enter 'demo1 D1o'. When finished with modifying input parameters, entering 'end', or pressing Ctrl+D (UNIX/Linux/Cygwin), or entering Ctrl+Z (MS native), or pressing Ctrl+Z (VMS) will start the calculation proper.
Alternatively, one can prepare an input file containing all input parameters
the values of which differ from the defaults hard-coded in TRANSIENT and in
a PDM. The same rules as for the interactive input apply:
one parameter per line; order of parameters is not important; in case of
duplicate entries, the last one is effective; for parameters not
present in the input file, default values are used.
Each line consists of a parameter name followed by its value, separated
by space or/and an equal sign. The full syntax of an input line is:
[comment char] [w] name [w] { [=][w] | [{=|w} [w] value [w [anything]]] }
Here 'w' represents any sequence of white spaces, [ ] delimit optional items,
and { | } alternative items. The only mandatory item is the parameter
name. A missing value is interpreted as a zero, null character or empty string.
Examples of input data files are in all demo/demoX subdirectories (data1, dataS1, data2, etc.). To use e.g. data1, specify it after the output file root name: such as 'demo1 D1o data1'.
The first character of each input line can be the comment character CmntC (see below). This feature allows to use directly a parameter output file (parOut), perhaps after some editing, as a new input data file. The comment character can also change inside an input file. In this way, whole groups of lines in the input file may be "switched" on or off between runs by editing a single line defining CmntC (see e.g. '#' and '%' in demo/demo1/data1) - the lines starting with a character that is not the current CmntC will be ignored, and the "Unknown input parameter name" warning issued.
To capture the list of all input parameters, their default values and
description into a file, type
'demo1 -p >& file_name' (UNIX) or 'demo1 -p > file_name' (MSDOS).
The file ends with whatever information (names, values, and description
of their purpose) on the problem-dependent input parameters the user supplies
in the PDM header file (in this case in demo1.h).
Description of all control input parameters can be found in the file controls.txt. It was generated by demo1 -c >& controls.txt. This list would be the same for all PDM, except that the default values of those control parameters that are exported from TRANSIENT to a PDM (see transien.h) may differ, as they can be reset in the PDM to suit better the modeled system.
If some of the right-hand sides of eqs. (1a) or of the left-hand sides
of eqs. (1b) depend explicitly on time, then
steady state has no meaning. However, in such a case,
steady >= 0 could be used for example to
calculate a possible final state corresponding to t = ![]() .
This could be achieved by setting all the terms in evalf
that depend explicitly on t to their limit values corresponding
to t =
.
This could be achieved by setting all the terms in evalf
that depend explicitly on t to their limit values corresponding
to t = ![]() when steady >= 0.
when steady >= 0.
The relation of some of the variables used in
TRANSIENT (transien.c) to the notation of section 2 is as follows:
tStart = t0, t = tl+1,
tt = | tl+1 - t0|,
ttOld = | tl - t0|,
Tau = ![]() ,
tStep = tl+1 - tl,
ttStep = |tStep|,
tStepInv = 1/(tl+1 - tl),
tStepInit is the initial value of ttStep,
tStepMax is the largest allowed value of ttStep.
,
tStep = tl+1 - tl,
ttStep = |tStep|,
tStepInv = 1/(tl+1 - tl),
tStepInit is the initial value of ttStep,
tStepMax is the largest allowed value of ttStep.
6.1. Pseudocode for the TRANSIENT V3.11 main function
Function main is located in module transien.c.
The user supplied PDM functions are shown in red.
void main(int argc, char **argv) {
< <Start CPU clocking; set up signal catching> >
neqns = get_neqns_etc();
read_input(argc, argv);
if(steady) Tau = 0.;
open_output(argc, argv);
/* Generates headers of all output files */
pr_par(-1);
/* Writes out all input parameter values into the par'Output' file */
generate_grid();
< <Allocate memory for c, c_o> >
Initialize(c, c_o);
if(*init_from_file != 0) read_profiles(init_from_file);
auxiliary_parameters_for_evalf();
startband(neqns,nnodes,c);
/* calls initNL3BANDV(...) */
if(steady) {
tStepInv = 0.;
c_o = c; /* Only in TRANSIENT, not in a PDM */
init_Other();
attempt = 1;
Try_steady_again:
/* runband invokes repeatedly evalf(node) */
if(runband(0.0) < 0) {
if(attempt < attemptMaxSteady) {
if(monitor) < <Report on the current attempt> >
Randomize(10*attempt+iter, 1e-3*max(| ck(j, l )|), c, c);
attempt+ +;
goto Try_steady_again;
}
< <Report FAILURE after attemptMaxSteady(=1000) attempts> >
exitTR(-2);
}
pr_profiles(iter);
update_Other();
pr_Other(0);
if(steady = = 1) exitTR(0);
else { /* steady==2 */
< <Restore Tau and c_o> >
auxiliary_parameters_for_evalf(); // 2nd time for steady=2
} /* End of: if(steady) */
}
/* Transient calculation: */
< <Set tSign = sign(tEnd-tStart) ;
transform the real time t to an always nonnegative
tt = |t - tStart|,
i.e., ttEnd = |tEnd - tStart|,
tOutInit = |tOutInit - tStart| > >
ttOld = ttOut = 0.;
tt = ttStep = tStepInit;
DttOut = tOutInit/nOutOTH;
highAttempts = 5;
< <etc.> >
init_Other() // 2nd time for steady=2;
< <Clock the beginning of the transient calculation; for stat'Output'> >
while(ttOld < ttEnd) {
for(k=1; k<=nOutOTH; k+ +) {
ttOut += DttOut;
if(ttOut >= ttEnd) { ttOut = ttEnd; k = nOutOTH; }
if(tt > tOut) { tt = ttOut; ttStep = ttOut - ttOld; }
/* This can happen when ttStep>DttOut */
do {
Try_again:
t = tSign * tt + tStart;
tStep = tSign * ttStep;
tStepInv = 1./tStep;
/* runband invokes repeatedly evalf(node) */
if(runband(t) < 0) {
if(ttStep > tStepMin) {
if(monitor>1) < <Report on the current attempt> >
attempt+ +;
< <Decrease ttStep, adjust tt, and reset c[j][k] > >
goto Try_again;
}
// Can happen only rarely, for singular matrices:
< <Report FAILURE> >
exitTR(-8);
}
cDiffM = ![]()
![]() | ck(j, l + 1) - ck(j, l )|
| ck(j, l + 1) - ck(j, l )|![]()
#if !NO_EXIT_m4
if(cDiffM = = 0.0) exitTR(-4);
/* A stable steady state was reached */
#endif
if(strict> =-1) Scale = cDifMxf(tt) / cDiffM; /* cDifMxf(tt) is determined by input
parameters cDifMxMode, cDifMxInit, cDifMxEnd */
if(strict= =1 && Scale<1. && ttStep>tStepMin) {
if(monitor>1) < <Report on the current attempt> >
< <Reduce current ttStep; interpolate c> >
attempt+ +;
goto Try_again;
}
if(attempt>1) highAttempts += attempt;
else if(highAttempts>1) highAttempts- -;
< <Adaptive time-stepping algorithm:
Determine the new time step using some or all of:
strict, Scale, highAttempts, magnitude of the last two steps.
Adjust the new time step if:
ttStep>tt (to limit time step initially)
or ttStep>tStepMax
or ttStep>ttOut and ttOld<ttOut.
> >
if(monitor) {
< <Print t, cDiffM> >
if(monitor>1) < <Print tStep, Scale> > else
< <Print attempt, iter> >
< <Print # of time steps, of calls to runband(), and of
all iterations since
the beginning of the run> >
}
< <Extrapolate to get initial guess for c[j][k] for new time> >
ApplyBounds(c);
< <Append diag'Output' file every now and then> >
tStep = tSign * ttStep;
i = update_Other();
if(i) out_Other(...); /* calls pr_Other(...) */
if(i<0) exitTR(1000-i);
#if RESETtStepAT99
if(i>1) < <Reset ttStep according to the value of i> >
else
#endif
{
if(tSign*tStep < ttStep) { /* tStep reduced in update_Other */
ttStep = tSign*tStep;
tt = ttOld + ttStep;
}
}
} while(ttOld < ttOut); /* End of: do */
out_Other(k<nOutOTH); /* calls pr_Other(k<nOutOTH) */
if(monitor= =0) < <Print summary information> >
} /* End of: for(k=1; k<=nOutOTH; k+ +) */
out_profiles(tt<ttEnd); /* calls pr_profiles(maxIterDone) */
if(tOutMulF > 1.) DttOut *= tOutMulF;
} /* End of: while(ttOld<ttEnd) */
endband();
exitTR(0);
} /* End of: main() */
6.2. Adaptive time-stepping algorithm
An heuristic adaptive time-stepping algorithm (ATSA) is implemented. When strict < 0, the time step is determined solely by nIter as described in Sec. 4. For all values of strict, the algorithm tries to choose the largest time step such that at most nIter NR iterations are needed in runband.
The current ATSA is based on the lengths of two previous time steps. From their ratio, and from whether the current number of iterations exceeds nIter or not, ATSA tries to determine a suitable next time step. This extrapolation is always biased towards larger time steps (it tries to push the step upwards whenever possible). If for the current time instant, NL3BANDV detects a really bad NR convergence, the time step is reduced, and another attempt at convergence is made. Too many recent repeated attempts signal that the time step has been increased too fast. The variable highAttempts keeps track of this (see Sec. 6.1). The larger its value is, the smaller is the upper limit on the maximum allowed time step increase. For further details, inspect the file transien.c.
With strict ![]() 0, in addition to what is described in the previous
paragraph, ATSA also compares cDiffM, which is the maximum change in
ck(x, t) over the current time step, with the maximum allowed by the user,
specified through the input parameters cDifMxMode, cDifMxInit, cDifMxEnd
that determine the form of the cDifMxf(tt) function (see Sec. 6.3).
If strict = 1, the algorithm makes sure that
cDiffM
0, in addition to what is described in the previous
paragraph, ATSA also compares cDiffM, which is the maximum change in
ck(x, t) over the current time step, with the maximum allowed by the user,
specified through the input parameters cDifMxMode, cDifMxInit, cDifMxEnd
that determine the form of the cDifMxf(tt) function (see Sec. 6.3).
If strict = 1, the algorithm makes sure that
cDiffM![]() cDifMxf(tt) almost "strictly".
cDifMxf(tt) almost "strictly".![]() If strict = 0, cDiffM may exceed
cDifMxf(tt) somewhat. The larger the cDifMxf(tt), the larger
the time steps (provided that nIter allows that) and the shorter
the total execution time, but also the larger the expected error.
If strict = 0, cDiffM may exceed
cDifMxf(tt) somewhat. The larger the cDifMxf(tt), the larger
the time steps (provided that nIter allows that) and the shorter
the total execution time, but also the larger the expected error.
One can watch the ATSA action with monitor ![]() 2.
2.
The NL3BANDV solver of the discretized nonlinear equations always tries to achieve the highest precision it can for a given time step, as described in Sec. 4. The values of strict, nIter and cDifMxf(tt) control the error caused by the discretization of time. Number and spacing of the x-grid nodes control the error introduced by spatial discretization.
The relaxed version of the ATSA algorithm corresponding to strict < 0 will essentially find the largest cDiffM (as a function of time) compatible with a given value of nIter. Often, this may already give very good results with a suitably chosen value of nIter.
Thus a recommended strategy for TRANSIENT V3.11 is to start with
strict < 0 and a sufficiently high value of nIter (at least 10).
If the resulting cDiffM is too large (check the contents of
the diag'Output' file), or a fatal failure with the exit code -8 is
encountered, first try to decrease the value of nIter.
If that alone will not help, use strict ![]() 0 and suitable
values of the parameters of cDifMxf() (initially again with a higher value
of nIter). In principle, one should repeat this process (decrease the values
returned by cDifMxf() further, and/or decrease the value of nIter)
until the results for concentrations do not change any more.
Of course, using very small values of cDifMxf(tt)
with strict
0 and suitable
values of the parameters of cDifMxf() (initially again with a higher value
of nIter). In principle, one should repeat this process (decrease the values
returned by cDifMxf() further, and/or decrease the value of nIter)
until the results for concentrations do not change any more.
Of course, using very small values of cDifMxf(tt)
with strict ![]() 0 can increase the execution time considerably.
The same may be true if using very small values of nIter.
0 can increase the execution time considerably.
The same may be true if using very small values of nIter.
cDifMxf() is actually a pointer to a function. This pointer is set at the end of read_input (in InOut.c) to point to a suitable function according to the value of cDifMxMode. To run a TRANSIENT-based program, it is enough to know that cDifMxf() returns the following values:
![]()
![]()
(linear interpolation)
![]()
(log-log linear interpolation equivalent to=
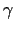
;
can be used only if tStart and tEnd have the same signs)
On termination, TRANSIENT returns the following status code:
0 : on successful termination;
-4 : when a steady state is reached in transient calculation (rare;
can be switched off by nozero NO_EXIT_m4
- see defs.h);
-3,-2,-1 : on improper initializations during TRANSIENT's startup;
-5 : when unsupported type of a model input parameter used in PDM;
-6 : when number of grid nodes changed after steady state calculation;
-7 : when number of grid nodes increased above the initial value;
-8 : when singularity encountered repeatedly in NL3BANDV;
> 100 : when a signal is caught (status = signal + 100);
1 ... 100 : can be set in a PDM using exitTR(status) to flag
various termination conditions.
1000+ | i|, where i < 0 is a negative return value of update_Other.
These exit codes will appear at the end of the stat'Output' file.
When you have to terminate TRANSIENT from a PDM, use exitTR(status)
instead of exit() (see demo/demo1/demo1.c for an example).
exitTR will update all the output files with the results available at the time of
termination, complete the last line of the diag'Output' (diag_out) file, and
generate the summary in the statistics file, stat'Output' (stat_out). Use exit
code 1 ![]() status
status ![]() 100, or 200
100, or 200 ![]() status
status ![]() 1000.
1000.
The above codes are passed through the C exit function, which accepts any
integer as its argument.
The contents of the shell exit status variable then equals this C exit
status modulo 256. E.g., in the Unix csh shell, 'echo $status' returns
values from -128 to 128, but in sh or bash shells, 'echo $?' returns
values from 0 to 255. Thus sh and bash will change the TRANSIENT's internal
exit statuses -8, -7, ..., -1 into 248, 249, ..., 255, respectively (this
has of course no effect on the termination codes and messages that may be
printed at the end of the stat'Output' file).
7. The details of writing your own PDM
PDM has two parts described in Secs. 7.1 and 7.2.
7.1. Header file with PDM-dependent input parameters
All information about the PDM-dependent input parameters is contained in a separate C header file. This file will be inserted (#include) into transien.h. In turn, transien.h is #included into the PDM source file(s). In this way the control and PDM-dependent parameters are integrated and handled in the same way. transien.h will extract from the PDM header file all the information needed for the declaration, input, output, and possible allowed-range checking of the PDM-dependent input parameters. Placing them into the PDM header file makes them global variables in the PDM source file(s), provided that the format of the beginning of source file(s) conforms to Sec. 7.2. They must not be declared again in the PDM source file(s).
The PDM header file may only contain arbitrary number of IN_PAR, IN_STRPAR and CHECK_PAR macros and C comments:
The PDM header file could be completely empty in the rare case that no model parameters will be changed between the runs. But it must always be present. Let us conclude this section with some examples of the entries of a PDM header file:
IN_PAR(L1,double,0.5,%g m,Thickness of medium 1)
CHECK_PAR(L1>0)
IN_PAR(interv2,int,45,%d,Number of intervals in "[L1,L1+L2]")
CHECK_PAR(interv2>0)
IN_STRPAR(frmt,10,"%.8g",format for double for concentrations & corr current & potential)
/* A space will be added at the beginning -> max usable length = 8: */
CHECK_PAR(strlen(frmt)<9)
/* description may be missing: */
IN_PAR(A,double,1.5e4,%g mol/cm
![]() 2,)
2,)
IN_STRPAR(BCr,8,"massBal",Type of formula for the zero flux RHS b.c.:
\n
\040
\040
\
massBal - full mass-balance equation for the last half interval;
\n
\040
\040
\
3point - standard three-point discretization formula)
CHECK_PAR(!strcmp(BCr,"massBal")
|| !strcmp(BCr,"3point"))
7.2. Source code for the user supplied functions
The list of the functions that must be defined in a PDM was
given in Sec. 5.2. They may be all placed in a single source
file, or may be distributed among several files. If there is only one such
source file, it must have the following two directives before all declarations:
#define PDM_H "PDMpath/PDMheader.h"
#include "TRDpath/transien.h"
If a PDM consists of more than one file, one of them (it does not matter which one)
must start again exactly as above. In all the other ("additional") source
files, an additional #define directive must precede the above two lines.
These additional source files must start as follows:
#define _ADDITIONAL_SOURCE_
#define PDM_H "PDMpath/PDMheader.h"
#include "TRDpath/transien.h"
Here `PDMheader.h' is the name you gave to the PDM header file described
in Sec. 7.1. `PDMpath' is its path relative to TRD, and
`TRDpath' is the path of TRD relative to the directory where the
PDM source file will be residing. Or one can use absolute paths.
Everything else in the above two (or three) lines is literal, including the
double quotes. PDM_H is a "place holder" for the name of the
PDM header file in the transien.h code. For example, for demo1, the
above directives are:
#define PDM_H "demo/demo1/demo1.h"
#include "../../transien.h"
Template for PDM source files is in the file PDMtemplate.c. In the rest of this section, one will find further details on how to write PDM source code.
All six functions get_neqns_etc, generate_grid, Initialize, read_profiles, auxiliary_parameters_for_evalf and initNL3BANDV are essentially initialization routines. They are invoked in TRANSIENT in the above order (see Sec. 6.1; read_profiles is called only if the init_from_file input parameter is assigned the name of an existing-file). All necessary initializations may be divided among them more or less arbitrarily, except that get_neqns_etc must return as its value the number of equations, neqns, the TRANSIENT's global variable nnodes must be set at the latest in the body of generate_grid, and Initialize and initNL3BANDV must pass through its arguments the pointers to certain arrays. And all the initializations that may depend on values changed in read_profiles must be deferred to auxiliary_parameters_for_evalf. Two other optional TRANSIENT's global variables, title and time_units, should also be defined preferably in get_neqns_etc so that they are available from the beginning in case that interactive help (?c-, ?ti, etc.) or the parameter lists (-d and -p command-line arguments) are required - these all are generated by read_input. Also the default (most often used) values of tStart, tEnd, tStepInit, tOutInit, tOutMulF, etc. and nOutOTH may be customized for the given problem by redefining them in get_neqns_etc, which may thus look like this:
int get_neqns_etc(void)
{
title = " TRANSIENT
\n
\
Demonstration No. 4
\n
\
Brusselator";
time_units = "";
tEnd = 50.;
tOutInit = 0.1;
tStepInit = 1e-4;
nOutOTH = 1;
return NEQNS;
}
or like this:
int get_neqns_etc(void)
{
...
time_units = "sec";
tOutMulF= 1.6;
return NEQNS;
}
If equidistant grid is used, generate_grid can be very simple, in addition to the definition of nnodes, it suffice to define the grid step h (TRANSIENT does not need to know the grid positions xj; in pr_profiles, one can use the formula xj = x0 + j*h). A more complicated example of a nonequidistant grid is in demo1.c.
The value of nnodes may be changed in a suitable place in a PDM. However, it must never exceed the value initially set in generate_grid. Eqs. (1a) are then solved only on the subset of the initial grid from node 0 up the the current node nnodes - 1. This feature can be useful in modelling moving boundary problems, with a moving boundary at the RHS end of the model.
The function Initialize is primarily intended to
initialize the concentrations.
Memory for the "old", c_o[j*N+k] = ck(j, l ), and "new",
c[j*N+k] = ck(j, l + 1), concentrations is allocated in TRANSIENT,
and the pointers to c and c_o are passed into the PDM
through the two arguments, cp and c_op, of Initialize.
As discussed in Sec. 3, in a PDM these arrays
can be declared as ROW *C, *C_o and one can refer
to them using the matrix notation C[j][k], etc. The pointers must
be properly typecast when passed between TRANSIENT and the PDM.
Two statements of the following type have to appear
in the body of Initialize:
C = (ROW *)cp;
C_o = (ROW *)c_op;
When neqns = 1, there is of course no need to define the ROW type and use
the typecast operators (see demo2a.c, demo2b.c and demo3.c).
C_o[j][k] must be assigned the initial values corresponding
to t = t0 for the given problem, and
C[j][k] some suitable initial guess for the initial time step
(C[j][k] ![]() C_o[j][k] will usually do).
C_o[j][k] will usually do).
The function initNL3BANDV also plays the role of an
interface, the interface between PDM and NL3BANDV. First, it transfers the
addresses of the BDA arrays from the PDM to NL3BANDV as described in
detail in Sec. 3.1. Second, it passes the addresses
of the vector of the function values ![]() and of the Jacobian submatrices
and of the Jacobian submatrices
![]() ,
, ![]() ,
, ![]() ,
, ![]() (sharing memory with
(sharing memory with ![]() ),
and
),
and ![]() (sharing memory with
(sharing memory with ![]() ) (see Sec. 2.4)
from NL3BANDV to PDM. These matrices are declared in nl3bandv.c as
pointers to double. If you wish to refer to them in PDM (mainly in evalf)
as to matrices (ROW), define in the PDM a set of pointers to ROW, e.g.,
ROW *AROW, etc., and use again the type cast operator,
) (see Sec. 2.4)
from NL3BANDV to PDM. These matrices are declared in nl3bandv.c as
pointers to double. If you wish to refer to them in PDM (mainly in evalf)
as to matrices (ROW), define in the PDM a set of pointers to ROW, e.g.,
ROW *AROW, etc., and use again the type cast operator,
A
ROW = (ROW *)A
double;
where Adouble is the formal argument of initNL3BANDVfor ![]() . Similarly for the
. Similarly for the ![]() and
and ![]() matrices.
XROW may be introduced as an alternative pointer to AROW,
similarly YROW = DROW. See PDMtemplate.c or
individual demos for more details.
matrices.
XROW may be introduced as an alternative pointer to AROW,
similarly YROW = DROW. See PDMtemplate.c or
individual demos for more details.
read_profiles can be used to overwrite any initializations in Initialize by reading the profiles from a file whose name is argument of this function. This is useful when an integration is to be continued with modified parameters, or after a system crash. read_profiles can simply be an "inverse" of the pr_profiles function described below. It can also be empty (take no action) if one plans to always start from the beginning.
The purpose of function auxiliary_parameters_for_evalf is to avoid repetitive calculations in evalf. Various subexpressions occurring repeatedly in evalf that need to be calculated only once can be declared as global variables and defined in auxiliary_parameters_for_evalf.
evalf calculates the Jacobian submatrices ![]() ,
,
![]() ,
, ![]() ,
, ![]() , and
, and ![]() , and the vector of the
function values
, and the vector of the
function values ![]() (see Sec. 2.4) for the j-th grid
point (the only argument of evalf) at the current guess for
concentrations, stored in the "new" C. Before a call to evalf, all
elements of matrices
(see Sec. 2.4) for the j-th grid
point (the only argument of evalf) at the current guess for
concentrations, stored in the "new" C. Before a call to evalf, all
elements of matrices ![]() to
to ![]() are zeroed. One thus has to set
in evalf() only all the nonzero elements. This is not true for F.
are zeroed. One thus has to set
in evalf() only all the nonzero elements. This is not true for F.
Note that in demo1.c and demo4.c the three "mixed" solutions
![]() (j - 1),
(j - 1), ![]() (j) and
(j) and ![]() (j + 1)
are stored in three vectors VM, V0 and VP (in some order).
Pointers to these vectors are stored in cBarM, cBar0 and
cBarP, such that cBarM points to the vector that contains
(j + 1)
are stored in three vectors VM, V0 and VP (in some order).
Pointers to these vectors are stored in cBarM, cBar0 and
cBarP, such that cBarM points to the vector that contains
![]() (j - 1) for the current j, cBar0 points to
(j - 1) for the current j, cBar0 points to
![]() (j) and cBarP to
(j) and cBarP to ![]() (j + 1). As
j is increased by 1, these pointers are simply rotated
(cBar0
(j + 1). As
j is increased by 1, these pointers are simply rotated
(cBar0 ![]() cBarM
cBarM ![]() cBarP
cBarP
![]() cBar0) instead of moving the contents of the vectors,
and only the vector pointed to by cBarP is updated.
cBar0) instead of moving the contents of the vectors,
and only the vector pointed to by cBarP is updated.
The implementation of evalf in demo1.c (or in demo2a.c,
demo2b.c and demo4.c) may hopefully be used without substantial
changes as a template for many problems with simple diffusion terms of the type
D ![]() ck/
ck/![]() x2 to calculate the contribution of the diffusion
terms and the time derivatives to
x2 to calculate the contribution of the diffusion
terms and the time derivatives to ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
On the other hand, the contribution of the reaction terms Rk of eq. (1a)
must generally be coded from scratch for each problem. In demo1.c it
is calculated in two separate functions, reaction_part for all nodes
except the last one, and reaction_part0 for the last node.
.
On the other hand, the contribution of the reaction terms Rk of eq. (1a)
must generally be coded from scratch for each problem. In demo1.c it
is calculated in two separate functions, reaction_part for all nodes
except the last one, and reaction_part0 for the last node.
The function pr_profiles is called at time instants determined by tOutInit and tOutMulF, and its role is to output the current concentration profiles to the 'Output'* file(s), i.e., to the output stream out (using e.g. the PR macro defined in incl_pri.h). Its single argument contains the maximum number of iterations used in a single time step since the last invocation of pr_profiles. The pr_profiles functions in demo1.c to demo4.c also invoke report_max_resid defined in nl3bandX.c. If steady=1, pr_profiles is called only once to output the steady-state profiles with its argument set equal to the number of iterations needed for the last successful attempt.
The functions init_Other, update_Other and pr_Other can be used to calculate any supplementary time-dependent quantities depending on the concentrations (such as the corrosion current, its integral over time, and the corrosion potential in demo1.c; comparison of the numerical and analytical solutions in demo2a.c and demo2b.c; the surface roughness in demo3.c; or the total amount of species k present in the model at time t, i.e., the integral of ck over x), and write them out conveniently at the end of the par'Output' file (using e.g. the Pm macro defined in incl_pri.h). pr_Other is called nOutOTH times more often than pr_profiles. The argument of pr_Other is set equal to 0 when the profiles are simultaneously written onto 'Output', and equal to 1 when they are not. Its value may be used in the body of pr_Other to avoid duplication of some output, or on the other hand, to add output for an additional time instant - see more notes in PDMtemplate.c; both pr_Other and pr_profiles may actually send alternate output to any of the two streams, or anywhere else, if user wishes so.
If one needs to do additional output at an arbitrary time, instead of using pr_profiles() and pr_Other(OnlyOther), one should use the out_profiles(NewFile) and out_Other(OnlyOther) functions (see the beginning of transien.h; NewFile is either 0 or 1, directing the profiles either into the same file as the previous ones, or to the next "out" file). These two TRANSIENT functions first check whether the profiles or the "Other" values may have already been printed for the same time, thus preventing the duplication of output.
The function init_Other is invoked just before the transient or the steady-state calculation starts, and may be used for any initializations needed for the calculation of the supplementary quantities. For steady = 2, init_Other is thus called twice - see how demo1.c handles this. If profiles are initialized from a previous output file, init_Other may perform some initializations from the corresponding par'Output' file, see demo1.c for an example.
The function update_Other is called after the successful completion of each time step and may be used for example for integrating some quantities over time. update_Other should normally return 0. If pr_Other() is to be executed immediately after the termination of update_Other, e.g. when a certain condition requires additional output, this can be achieved by update_Other() returning a nonzero integer. Moreover, if it returns a negative number, i < 0, the execution is terminated immediately with the exit code 1000 - i. When the macro RESETtStepAT99 is set during the compilation (see the file defs.h), the i > 1 return values of update_Other() also have the following additional effect: if i = 99, the next time step is reset to its initial value of tStepInit, and for all other i > 1, it is decreased by the factor of 10i. At the same time, the ATSA is re-initialized.
One can also use update_Other() to reduce the magnitude
of the next time step tStep explicitly to a certain value without
re-initializing the ATSA. For example, if the value of a quantity BCv
has to be changed at time t1, put in the body of update_Other()
the following lines:
static int t1Flag = 1;
...
if(t1Flag) {
if(t >= t1) { BCv = BCv1; t1Flag = 0; }
else if(t+tStep >= t1) tStep = t1-t;
}
The else if condition gets satisfied first and as a result tStep is
reduced so that the next time step ends exactly at time t1. During the
next invocation of update_Other() (at the end of the next time
step), the preceding if condition is satisfied, and the value of BCv
changed to BCv1 exactly at t=t1. Here we assume that time is
positive and increasing. t1 and BCv1 can be variable model
parameters to appear in the PDM header file.
For a steady-state calculation, update_Other and pr_Other are called only once after the completion of the calculation.
All three functions init_Other, update_Other and pr_Other can be empty. If you plan to use TRANSIENT for both the steady-state calculation and the transient solution, you may wish to use the switch steady (exported from transien.c) in the functions pr_profiles, init_Other, update_Other and pr_Other to differentiate their actions for the two types of calculations (see the supplied demos). Always use the "old" solution c_o in all these output functions.
Four demonstration examples (demos for short) of TRANSIENT applications are provided. Each is located in a separate directory demo/demoX, X=1,2,3,4. Start exploring the demo directory tree by reading the demo/0readme.txt file. Demo 1 is a relatively simple example of the rather complicated systems that TRANSIENT can handle. However, it may be too complicated as a starting point for the exploration of this package. Demos 2 and 4 provide much simpler starting points.
Demos 1, 2 and to some extent (for some parameter values and/or time ranges) also demo 4, are types of problems when the evolution of concentration (dependent variable) profiles is uneven in time, and thus the use of TRANSIENT with its adaptive time-stepping algorithm is of big advantage for such problems. On the other hand demo 3 in its original formulation requires constant time step. Nevertheless, TRANSIENT seems to handle even such a problem quite satisfactory - it automatically keeps time step practically constant.
8.1. Demo 1. Uniform corrosion of a metal surface in contact with two consecutive porous media
The files demo1.h and demo1.c in demo/demo1
are an example of the PDM for the following problem![]() with neqns = 6:
with neqns = 6:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Here all the concentrations ci are functions of x and t. Initial conditions are
![]()
![]()
![]()
The first medium is in contact with a uniformly corroding copper wall
at x = 0, and this electrochemical corrosion process determines boundary
conditions ![]() k, left for the diffusing species at x = 0.
These involve the corrosion current related to the diffusion flux of the
first two species:
k, left for the diffusing species at x = 0.
These involve the corrosion current related to the diffusion flux of the
first two species:
![]()
![]()
![]()
![]() k, right at x = xright are constant concentration
b.c.:
k, right at x = xright are constant concentration
b.c.:
![]()
![]()
![]()
The region near x = 0 is very important because the electrochemical reactions (eqs. (27) and (28)) that drive the whole process take place there. It is thus desirable to have a much finer grid near x = 0 than near xright. To this end a "geometrical progression" grid is used, with xj+1 - xj = f (xj - xj-1) where f is constant for all j, i.e.,
![]()
The input for generate_grid in demo1.c are the numbers of grid
intervals in (0, L1), interv1, and in (L1, L1 + L2), interv2.
generate_grid then determines x1 and f such that one grid point
lies exactly on the interface: xinterv1 ![]() L1. Note that for the
geometrical progression grid, all coefficients on the right-hand side of eq.
(4) are simply multiplied by 1/f2 (f2 is called fsq in
demo1.c) when j is increased by 1. These coefficients are stored
in demo1.c in variables ja2 and jd2.
L1. Note that for the
geometrical progression grid, all coefficients on the right-hand side of eq.
(4) are simply multiplied by 1/f2 (f2 is called fsq in
demo1.c) when j is increased by 1. These coefficients are stored
in demo1.c in variables ja2 and jd2.
For the internal nodes in the two media, we can simply divide eqs. (19), (20)
and (22) by ![]() or
or ![]() and get a set of equations
of type (1a) and discretize them as described in Sec. 2.2
or Sec. 2.3 - for the internal nodes both discretization
approaches will give identical results. At j = interv1, the "coefficients"
(
and get a set of equations
of type (1a) and discretize them as described in Sec. 2.2
or Sec. 2.3 - for the internal nodes both discretization
approaches will give identical results. At j = interv1, the "coefficients"
(![]() , etc.) in eqs. (19-24) have a discontinuity, and to derive
the discretized Fkinterv1, the best way is to use the mass-balance
approach of Sec. 2.3, i.e., to start from the integral form of
the mass-balance equations (19-24) for the small region (L1 -
, etc.) in eqs. (19-24) have a discontinuity, and to derive
the discretized Fkinterv1, the best way is to use the mass-balance
approach of Sec. 2.3, i.e., to start from the integral form of
the mass-balance equations (19-24) for the small region (L1 - ![]() /2, L1 +
/2, L1 + ![]() /2). Note that after dividing the diffusing equations (19), (20)
and (22) by
/2). Note that after dividing the diffusing equations (19), (20)
and (22) by ![]() , their reaction terms can be written in the form
, their reaction terms can be written in the form
![]()
![]()
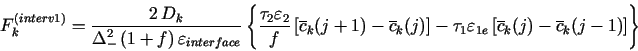
![]()
![]()
Note that the reaction term in eq. (31) has exactly the same form as at the
interior nodes, except that ![]() is replaced by
is replaced by
![]() . The same result is obtained for the
nondiffusing eqs. (21) and (23). Discretizing these equations in the
same way as the diffusing ones above, one gets
. The same result is obtained for the
nondiffusing eqs. (21) and (23). Discretizing these equations in the
same way as the diffusing ones above, one gets
![]()
For the j = 0 node (LHS boundary conditions), the 3-point formulas (6a) were used directly in eqs. (27-29) without much thought when TRANSIENT was first used to study systems of this type in 1995. The resulting discretized equations then served as the expressions for Fk(0). This was implemented in the old demo 1 source file. The old approach did not enforce mass-conservation within the surface region (0, x1/2). However, this region is usually very tiny, and thus the resulting error could be expected to be rather small.
In the meantime I have switched over to using the more consistent mass-balance discretization also in the surface region even in cases much more complicated than that eq. (28). Such an approach is finally implemented also in the current demo1.c. Mass-balance discretization of the "boundary conditions" should give better results whenever the diffusion fluxes (slopes of ck) are high in the surface regions. In the demo 1 case, the only noticeable (but quite small) difference between the old results and the current ones is in the corrosion potential in the first 150 years (see below).
In the mass-balance approach for the j = 0 node, one has to integrate
eqs. (19-24) also in (0, x1/2). The result of this integration can be
obtained from eq. (30) after replacing in it ![]() by
by
![]() or
or ![]() as appropriate,
as appropriate, ![]() by
by ![]() ,
xj by 0,
,
xj by 0, ![]() by 0, and
by 0, and ![]() by x1.
For
by x1.
For ![]() (
(![]() , t), one can again use
eq. (7a), but for
, t), one can again use
eq. (7a), but for ![]() (0, t), eqs. (27) and (29)
must be used. This gives
(0, t), eqs. (27) and (29)
must be used. This gives
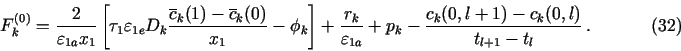
![]()
Finally, icorr has to be expressed as a function of c0(0, t) and
c1(0, t) by solving eq. (28). It is a cubic equation in icorr,
and one can show that it always has a single nonnegative real root (because
A1![]() 0, A2
0, A2![]() 0), which gives the nonnegative icorr.
It is however easier to solve it numerically using Newton's method, than to
use the analytical formulas expressing the real roots of a cubic equations
in terms of complex numbers. Such numerical solution is implemented in
demo1.c in the function iCorr_f (to be used in init_Other()
and pr_Other()), and also at the beginning of the j = 0
branch in evalf(), where in addition to icorr also the derivatives
of icorr with respect to c0 and c1 are needed.
0), which gives the nonnegative icorr.
It is however easier to solve it numerically using Newton's method, than to
use the analytical formulas expressing the real roots of a cubic equations
in terms of complex numbers. Such numerical solution is implemented in
demo1.c in the function iCorr_f (to be used in init_Other()
and pr_Other()), and also at the beginning of the j = 0
branch in evalf(), where in addition to icorr also the derivatives
of icorr with respect to c0 and c1 are needed.
In demo 1, init_Other calculates the initial value of icorr,
update_Other calculates the time integral ![]() icorrdt,
and pr_Other outputs to the par'Output' file both of these
quantities and also the corrosion potential
icorrdt,
and pr_Other outputs to the par'Output' file both of these
quantities and also the corrosion potential
![]()
A possible way to reduce the number of operations in evalf is to include
the factor ![]() in the definitions of all Fk(j). This
will eliminate the factor New=1 -
in the definitions of all Fk(j). This
will eliminate the factor New=1 - ![]() (see the paragraph below eq. (12))
from all terms of all non-zero elements of the Jacobian matrices A, B, D,
X and Y, and add the factor 1/New only to the contributions of the
time derivatives to the diagonal elements of B. This is not implemented
in demo1.c, but it is recommended for more complicated systems with
a large number of non-zero elements in the Jacobian matrices.
(see the paragraph below eq. (12))
from all terms of all non-zero elements of the Jacobian matrices A, B, D,
X and Y, and add the factor 1/New only to the contributions of the
time derivatives to the diagonal elements of B. This is not implemented
in demo1.c, but it is recommended for more complicated systems with
a large number of non-zero elements in the Jacobian matrices.
Names of variables used in demo1.c closely follow the notation used in eqs. (19-25) (e.g., km11 represents k-11, etc.).
Demo 1 sample results obtained with TRANSIENT V3.0 are
in the directory demo/demo1/out. However, they do not differ substantially
from the older V2.51 results, retained in the demo/demo1.V2.51/out.
Thus the rest of this section was left unchanged, referring to the old
V2.51 results:
Discussion of the sample results from demo/demo1.V2.51/out
(August 2001)
An example of input data for the steady-state calculation is the file dataS1. The corresponding output is in files S, parS, etc. Number of iterations needed to obtain this steady state may be different on different machines because even a small difference in the precision of the floating-point arithmetics may show up. If more than one attempt was made, a much larger difference in the number of iterations may be observed due to possibly different implementations of the basic random number generator rand, which is used to generate initial guess for individual attempts at calculating the steady state. Of course, the resulting steady state must be (within the specified tolerance) identical on different machines.
The steady state obtained with dataS1 is stable. One can check this by using this state as the initial state for a transient calculation (e.g., change steady 1 in dataS1 to steady 2, and rerun for an arbitrary tEnd). However, for the parameter values used, it takes about 390 million years (of real time t) to reach this steady state from the initial state of eq. (25).
An example of the input data file for transient calculation is data1.
Model parameters are the same as in the steady-state input file
dataS1. To get some interesting results, one has to specify tEnd
larger than 4,733,640,000 sec (150 a). This is the time when
the oxygen concentration (c0) drops to zero at x = 0. Therefore
corrosion stops (icorr = 0 by eq. (28)) at that moment.
Within about the next 50 a, all oxygen that was initially present in
the first, rather porous, medium (clay) is used up.
The second medium represents a high quality rock with a very small
porosity through which additional oxygen can diffuse extremely
slowly from groundwater flowing relatively fast through a major
fracture in the rock assumed to be situated at the RHS boundary (i.e.,
the boundary conditions at x = xright = L1 + L2 simulate the surface of a large
fracture). The dissolved Cu(II) concentration (c3) reaches
a maximum at x = 0 in about 30 a. It then slowly decreases and spreads
from the corroding surface. Up to the time of about 5000 a, buildup of the
Cu(I) concentrations (dissolved c1 and precipitated c2) takes place.
At about 350,000 years, oxygen concentration drops to zero throughout the whole
model except for the tiny vicinity of the fracture zone at the RHS boundary.
After that, it takes hundreds of millions of years before
the excess c1 diffuses out of the system through its RHS boundary before
the steady state is being approached. During this time, all oxygen coming in
through the x = xright boundary is consumed in the nearest vicinity of
xright, and c0 = 0 in the rest of the system. Thus also icorr = 0.![]() Only when the steady state is finally being approached, nonzero c0 front
again reaches x = 0, and very slow corrosion represented by a tiny icorr
resumes.
Comparing parLONG and LONG33 with parS and S, one can
see that the corrosion potential settles to the steady-state value of -0.731 V
at about 390 million years. At the same time the concentration profiles
also assume the form of the steady-state from file S.
Only when the steady state is finally being approached, nonzero c0 front
again reaches x = 0, and very slow corrosion represented by a tiny icorr
resumes.
Comparing parLONG and LONG33 with parS and S, one can
see that the corrosion potential settles to the steady-state value of -0.731 V
at about 390 million years. At the same time the concentration profiles
also assume the form of the steady-state from file S.
Increasing interv1 and interv2 (decreasing internode spacings) above the values in data1 can still improve some details of the profiles for some ck.
Validation of the demo 1 results by comparison
with a crude analytical model
Certain observations about the nature of the numerical solution at long times are used here to construct an analytical model confirming the validity of the demo 1 results (time needed to reach the steady state).
Note that in the time interval from about 350,000 a to about 180×106 a (output files LONG22 to LONG31), the controlling process is the slow diffusion of Cu(I) out of the model. One can verify this by solving only eqs. (20) and (21) with c1 and c2 initialized with the results of the LONG run for t = 349.5×103 a (i.e., from the file LONG22). To achieve this, run demo1 with the input file data1cu. Sample output from such a run are the files parLONGcu, LONGcu1 and LONGcu7.
demo1.c is now capable, in addition to solving the full model with six
species, also to solve its two simpler subsets. The new input parameter
onlyCuI serves as the switch between these three cases:
onlyCuI=0 gives the full model;
onlyCuI=1 solves eqs. (20) and (21) only (with all other concentrations
set to 0); and onlyCuI=2 solves eq. (20) only, with k5 = 0, after all
the initial c2 was converted instantaneously into c1
(c1 + c2/![]()
![]() c1).
The values onlyCuI=1 and 2 are permitted only with the initialization
from a previous profiles file.
In data1cu, onlyCuI=1 and init_from_file=LONG22.
c1).
The values onlyCuI=1 and 2 are permitted only with the initialization
from a previous profiles file.
In data1cu, onlyCuI=1 and init_from_file=LONG22.
Comparing the file LNGcui (the two species subset solution) with LONGi+22, i=1,2,...,8, shows that they both give exactly the same c1 and c2 values (3rd and 4th columns). c1 starts to differ near x = xright only between files LNGcu9 and LONG31 (i.e., for t = 179×106 a, when nonzero c0 starts to spread from x = xright into the interior).
This excellent agreement is due to the fact that the two species subset correctly represents the dynamical equilibrium between the dissolved and precipitated Cu(I). Somewhat worse agreement is obtained with onlyCuI=2 when all c2 is instantaneously converted into c1 at the beginning of the run.
Note further that between about 2.7×106 a and 180×106 a, c1 is practically constant in the first medium, and in the second medium it decreases almost linearly to zero. Thus in this time interval, one can approximate c1 roughly as follows:
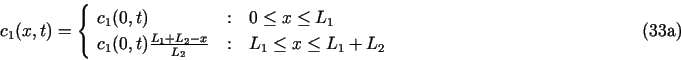
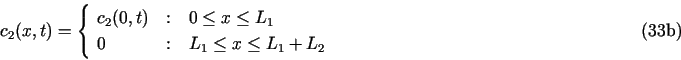
![]()
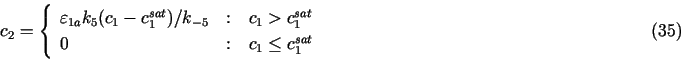
M(t) can change only as a result of the diffusion of c1 through the RHS boundary. This diffusion outflow is proportional to the slope of c1(x, t) (at xright):
![]()
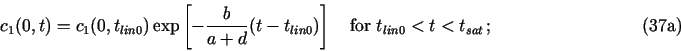
![]()
![]()
![]()
![]()

The following table compares the numerical values of c1(0, t) obtained in the LONG run (using input data file data1) with the approximate analytical results of eq. (37).
| c1(0, t) (mol/m3) | |||
| Time (106 a) | Full model | Eq. (37) | |
| 2.796203 (tlin0) | LONG25 | 0.245 | 0.245 |
| 5.592405 | LONG26 | 0.214 | 0.222 |
| 11.18481 | LONG27 | 0.167 | 0.182 |
| 22.36962 | LONG28 | 0.102 | 0.122 |
| 44.73924 | LONG29 | 0.0343 | 0.0476 |
| 89.47849 | LONG30 | 0.00392 | 0.00648 |
| 178.9570 | LONG31 | 5.45×10-5 | 1.20×10-4 |
| 357.9139 | LONG32 | 1.37×10-8 | 4.13×10-8 |
| 382.7401 | 1.37×10-8 | ||
Given the nature of the approximations used to obtain eq. (37), the agreement of the two solutions in the above table is rather good, confirming that the TRANSIENT based programs give realistic time scales for the modeled processes. The fact that eq. (37) gives solution that decreases slower with time than the numerical solution, only further confirms a good performance of TRANSIENT. Namely, eq. (33a) does not strictly satisfy eq. (20). Compared to eq. (33a), the true c1 is a slightly convex function, the slope of which at x = xright is more negative than that of eq. (33a). Steeper slope results in faster diffusion of c1 out of the system, and thus somewhat shorter duration of the modeled processes.
8.2. Demo 2. Gas generation and diffusion
This is a rather trivial application of TRANSIENT. It is a case for which
some analytical results are available, and can thus be compared with the
numerical values obtained by TRANSIENT. Different handling of an interface in
the interior of the system is discussed here (see the input parameter INTERFACE). This is also related to the type of the grid used. The two
demonstration PDM's in the subdirectory demo/demo2, demo2a.c and
demo2b.c differ only in the spatial grid used. Because neqns = 1, this
case allows to compare the speed of nl3band1.c with that of nl3bandv.c - to link demo2a.c or demo2b.c with nl3bandv.c
instead of nl3band1.c, no changes need to be done in the
PDM.![]()
The set of equations solved in this example is:
![]()
![]()
![]()
![]()
![]()
Possible questions to be answered: Does the maximum steady-state concentration exceed the critical explosive concentration of hydrogen in the air? If so, how long does it take to reach the critical concentration? To answer the second question we need to know the transient solution.
Analytical steady-state solution of eqs. (38-40) is
![]()
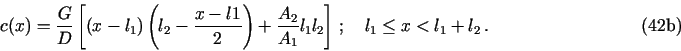
The transient solution is more complicated. It is easy to get a closed formula for the Laplace transform,
![]()
![]()
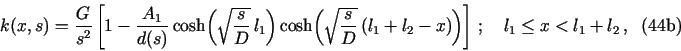
![]()
Note that eq. (43) involves integration to t = ![]() . TRANSIENT gets
numerical results for c(x, t) only for t
. TRANSIENT gets
numerical results for c(x, t) only for t ![]() (0,
(0,![]() ). pr_Other
assumes when calculating the tail of integral in eq. (43) that a steady
state was already achieved at t =
). pr_Other
assumes when calculating the tail of integral in eq. (43) that a steady
state was already achieved at t = ![]() , i.e., that
c(x, t) = c(x,
, i.e., that
c(x, t) = c(x,![]() ) for t >
) for t > ![]() . If it seems that the steady
state has not yet been reached (that the last two profiles are not identical),
a warning appears in the par'Output' file. For the purpose of the above
comparison, make sure that tEnd is large enough. Remember that for
small tEnd and small s, the "numerical" column for k(x, s)
in par'Output' is wrong due to the above tail approximation.
. If it seems that the steady
state has not yet been reached (that the last two profiles are not identical),
a warning appears in the par'Output' file. For the purpose of the above
comparison, make sure that tEnd is large enough. Remember that for
small tEnd and small s, the "numerical" column for k(x, s)
in par'Output' is wrong due to the above tail approximation.
Discretization of the interface condition (40):
They are two possibilities:
(i) The standard (simple) approach is to approximate the left and right
derivatives in eq. (40) by
![]()
![]()
Approach (i) was not used in demo1 at all. Here it is included because the existence of the (semi)analytical solution makes it possible to compare it quantitatively with approach (ii). The switch between the two approaches in demo2a.c and demo2b.c is provided by the input parameter INTERFACE. Comparing the results obtained with different values of INTERFACE, one can see that approach (ii) always gives better results, as expected. The RHS of eqs. (45) are indeed poor approximations for the left and right derivatives at the interface, but they are natural approximations for the derivatives at midpoints between the nodes (cf. eq. (7a) and (7b)).
demo2a.c uses a single equidistant grid for the whole
region 0 ![]() x
x ![]() l1 + l2. This is obviously not the best choice, as
in such a grid the interface at x = l1 will not generally coincide with
a grid point. It is used to explore the consequences of such a bad choice.
Let h be the distance between the
two neighboring nodes, j the index of the node nearest to the
interface at l1, and
l1 + l2. This is obviously not the best choice, as
in such a grid the interface at x = l1 will not generally coincide with
a grid point. It is used to explore the consequences of such a bad choice.
Let h be the distance between the
two neighboring nodes, j the index of the node nearest to the
interface at l1, and ![]() = l1 - xj (|
= l1 - xj (|![]() |
| ![]() h/2) the
difference in the positions of the interface and the nearest grid node.
h/2) the
difference in the positions of the interface and the nearest grid node.
In this case ![]() =
= ![]() = h in eqs. (45). When INTERFACE = 2
or 3, condition (40) is used directly (approach (i))
and F0(j) of eq. (8) is
= h in eqs. (45). When INTERFACE = 2
or 3, condition (40) is used directly (approach (i))
and F0(j) of eq. (8) is
![]()
![]()
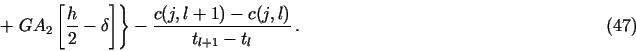
Apparently, the larger the |![]() |, the poorer the agreement
one can expect between the numerical and analytical results,
because the change in the slope
of c occurs at the interface, not at the node xj. To verify
this, INTERFACE = 0 and 2 correspond to the original system
as described above, whereas INTERFACE = 1 and 3 to a
modified system in which the lengths l1 and l2 are adjusted
(changed to l1'
|, the poorer the agreement
one can expect between the numerical and analytical results,
because the change in the slope
of c occurs at the interface, not at the node xj. To verify
this, INTERFACE = 0 and 2 correspond to the original system
as described above, whereas INTERFACE = 1 and 3 to a
modified system in which the lengths l1 and l2 are adjusted
(changed to l1' ![]() xj = l1 -
xj = l1 - ![]() and l2' = l2 +
and l2' = l2 + ![]() )
so that the total length of the system remains the same, and a
grid point lies on the interface and thus
)
so that the total length of the system remains the same, and a
grid point lies on the interface and thus ![]() = 0.
= 0.
The supplied sample input file demo/demo2/data2 corresponds to
INTERFACE = 0. In this case ![]()
![]() 0, and the agreement
between analytical solution and TRANSIENT's numerical results
is not good enough both for the steady-state and transient solutions.
If you switch to INTERFACE = 1 (adjust lengths) in the input
file, you will get a perfect agreement for the steady state (in all
decimal digits printed) and the best agreement possible (better than
for all the other values of INTERFACE) for the transient solution.
0, and the agreement
between analytical solution and TRANSIENT's numerical results
is not good enough both for the steady-state and transient solutions.
If you switch to INTERFACE = 1 (adjust lengths) in the input
file, you will get a perfect agreement for the steady state (in all
decimal digits printed) and the best agreement possible (better than
for all the other values of INTERFACE) for the transient solution.
If you switch to INTERFACE = 2 or 3 (eq. (46); approach (i)), the agreement is much worse than when using eq. (47), both for the modified and the original systems.
The conclusion is: for the best results, use the mass-balance discretization at the interface, and put a grid point on the interface.
Adjusting length as in demo2a.c (INTERFACE = 1 or 3) may not always be an ideal solution when the exact dimensions of the system do matter. It results in the best numerical solution, but for a slightly different system than the specified one. That is why in demo2b.c a nonequidistant grid is tested that always has a grid point at the interface for arbitrary l1 and l2. Everything else is the same as in demo2a.c.
demo2b.c uses only two different grid steps: h1 in (0, l1)
and h2 in (l1, l1 + l2). Then ![]() = h1 and
= h1 and ![]() = h2,
and eq. (46) is replaced by
= h2,
and eq. (46) is replaced by
![]()
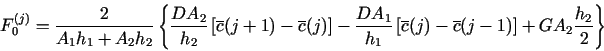
![]()
For compatibility with demo2a.c, INTERFACE can again be set to all four values 0 to 3, but 0 and 1 (and 2 and 3) will give identical results (now there is nothing to adjust when INTERFACE = 1 or 3). Again, INTERFACE = 0 (mass-balance discretization used at the interface; approach (ii)) gives perfect or near-perfect agreement between numerical and analytical concentrations, whereas INTERFACE = 2 (direct continuity-of-flux condition; approach (i)) gives much poorer agreement.
Alternatively, one could also use the "geometrical progression"
grid as in demo1.c, especially when l1 ![]() l2 (to have
enough points in the important inlet region where concentration
changes rapidly, without introducing a very large difference
in the neighboring grid steps at the interface).
l2 (to have
enough points in the important inlet region where concentration
changes rapidly, without introducing a very large difference
in the neighboring grid steps at the interface).
Finally, in both demo2a and demo2b there is a possibility for the last node to switch between the 3-point discretization of eq. (6b) for the second condition of eq. (39), and the mass-balance discretization, given for demo2a by
![]()
8.3. Demo 3. Stochastic surface growth
The following single equation for the dependent variable h(x, t) is solved:
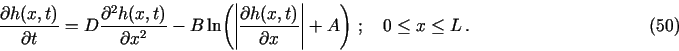
What is actually studied in ref. [15] is the discretized version
of eq. (50) corresponding to ![]() = 1 (fully implicit scheme),
the unit grid step, i.e., xj
= 1 (fully implicit scheme),
the unit grid step, i.e., xj ![]() j; j = 0, 1,..., L, and
periodic boundary conditions. TRANSIENT cannot at present
handle periodic boundary conditions (this would require a
modification of nl3bandX.c that would almost double
the size of its work memory). Instead, in demo3.c there is a
choice of von Neumann (input parameter bc = 0) or Dirichlet
(bc = 1) boundary conditions identical at the two ends of
the system. In both cases, the boundary value is supplied
through the input parameter bcValue. Because of this difference
in the boundary conditions, one cannot expect that the character of
the surfaces generated by TRANSIENT will be exactly the same
as in ref. [15].
j; j = 0, 1,..., L, and
periodic boundary conditions. TRANSIENT cannot at present
handle periodic boundary conditions (this would require a
modification of nl3bandX.c that would almost double
the size of its work memory). Instead, in demo3.c there is a
choice of von Neumann (input parameter bc = 0) or Dirichlet
(bc = 1) boundary conditions identical at the two ends of
the system. In both cases, the boundary value is supplied
through the input parameter bcValue. Because of this difference
in the boundary conditions, one cannot expect that the character of
the surfaces generated by TRANSIENT will be exactly the same
as in ref. [15].
Also in ref. [15] the discretized finite difference equation
does not correspond exactly to eq. (50) (eq. (4) of ref. [15]).
In ref. [15], the factor ![]() was omitted in the
difference formula for
was omitted in the
difference formula for ![]() .
This has the same effect as multiplying A by 2. In demo3.c,
eq. (50) is discretized consistently (using the unit grid step
again). Thus, A = 0.001 of demo3.c corresponds
to A = 0.002 in the figure captions of ref. [15], etc.
.
This has the same effect as multiplying A by 2. In demo3.c,
eq. (50) is discretized consistently (using the unit grid step
again). Thus, A = 0.001 of demo3.c corresponds
to A = 0.002 in the figure captions of ref. [15], etc.
The functions init_Other and pr_Other are used to calculate the "roughness" of the surface defined as
![]()
With ![]() = 1 and bc = 0 (von Neumann), TRANSIENT can
generate surfaces resembling closely those of ref. [15]
(see data3 in subdirectory demo/demo3).
= 1 and bc = 0 (von Neumann), TRANSIENT can
generate surfaces resembling closely those of ref. [15]
(see data3 in subdirectory demo/demo3).
As ![]() is decreased, the generated surfaces can change considerably.
Also any slight change in the adaptive time-stepping algorithm during
TRANSIENT's evolution usually led to a big change in the appearance of the
generated surfaces. This is illustrated by the enclosed figures
(files w1.ps and w2.ps) which compare the results obtained for
w(t) with four different previous versions of TRANSIENT. It confirms the
claim of ref. [15] that the features of the surfaces produced are the
consequence of the discretized finite difference equation, not of the
original eq. (50).
is decreased, the generated surfaces can change considerably.
Also any slight change in the adaptive time-stepping algorithm during
TRANSIENT's evolution usually led to a big change in the appearance of the
generated surfaces. This is illustrated by the enclosed figures
(files w1.ps and w2.ps) which compare the results obtained for
w(t) with four different previous versions of TRANSIENT. It confirms the
claim of ref. [15] that the features of the surfaces produced are the
consequence of the discretized finite difference equation, not of the
original eq. (50).
The Dirichlet boundary conditions (bc = 1) will anchor the surface at both ends, and thus generate a very different type of surface: a smooth growing "tip" (see data3.tip input file) that ends up in a steady state.
Steady-state calculation for bc = 0 will always fail
(even if one changes the code in demo3.c to initialize h(x)
directly to the trivial steady state h(x) = (1 - A)x and specifies
bcValue = 1 - A). This can be proved exactly: in this
special case the matrix ![]() of eq. (15) is always
singular when bc = 0, irrespective of the initial guess for
h(x). The same is true when the 3-point difference formulas used
in the boundary conditions are replaced by the 2-point formulas, or
when different boundary values (slopes of h(x)) are used at the
two ends.
of eq. (15) is always
singular when bc = 0, irrespective of the initial guess for
h(x). The same is true when the 3-point difference formulas used
in the boundary conditions are replaced by the 2-point formulas, or
when different boundary values (slopes of h(x)) are used at the
two ends.
The nonlinear Brusselator model [16] is often used in mathematical biology to study morphogenesis (e.g., [17]). It consists in the following two equations:
![]()
![]()
Rate constants a, b, c and d of eqs. (51) correspond in demo4.c to input parameters aa, bb, cc and dd.
The zero-flux b.c. at both model ends are again handled in two ways: directly using the 3-point discretization formulas of Sec. 2.2 or the mass-balance discretization of Sec. 2.3. The input parameter BC having legal values `3point' and `massBal' is provided to switch between these two options. The concentration profiles obtained with BC = 3point and BC = massBal differ significantly near x = 0 and x = L when X and Y vary rapidly with x in these regions, which they often do. Thus in this case the improvement introduced by the use of the full mass-balance equation at the boundary nodes may be significant. On the other hand, when the concentration profiles are nearly constant near the end of the domain of eq. (1a) (such as in demo 2), both approaches give the same results.
The behavior of the solutions of eqs. (51) can vary considerably depending on the values of the parameters involved. One can get an idea of what type of transient behavior to expect for a given set of DX, DY, a, b, c and d by performing the stability analysis of the linearized eqs. (51) (these linearized equations are called the Turing model, first studied by A. M. Turing [18] of the Turing machine fame).
There may be more than one steady state (there is always at least the trivial steady state X(x) = a/d, Y(x) = bd /ac). For example with TRANSIENT V1.3, the default parameter values (when starting demo4 by 'demo4 outfile_name', then typing 'steady 1', then 'end') gave a steady state consisting of two periods of a sine-like wave. The same parameters gave transient solution in which the initial random nonuniformity in space is slowly amplified until a single peak in X (corresponding to a minimum in Y) develops. With TRANSIENT V2.04, one got the trivial steady state in both cases.
On the other hand, when data4 was used as the input file in TRANSIENT V2.04, the results went fast to a single-peak steady state, whereas with TRANSIENT V1.3, the initial nonuniformity disappeared rather quickly, and then the spatially uniform X and Y seemed to slowly approach the trivial-steady-state values. For the same input parameters, the three steady-state input files data4.s1, data4.s2 and data4.s3 differ only in the initial random guess for X and Y. They usually give three different steady states - the first one is the trivial steady state, the two other are mirror images of each other (or S2 can be identical with S3, depending on the machine); see the files in demo/demo4/out.
References:
[1] R. Spotnitz, "NL3BAND", Technical Software Distributors, Charlotte, NC, 1994.
[2] J. Newman, "Electrochemical Systems", Prentice-Hall, Englewood Cliffs,
N, 1973.
[3] R.E. White, "On Newman's Numerical Technique for Solving Boundary
Value Problems", Ind. Eng. Chem. Fundam. 17, No. 4, 1978.
[4] T.V. Nguyen and R.E. White, "A Finite Difference Procedure for Solving
Coupled, Nonlinear, Elliptic Partial Differential Equations",
Comput. Chem. Engng. 11, 543-546, 1987.
[5] M. Matlosz and J. Newman, "Solving 1-D Boundary-Value Problems with
BandAid: A Functional Programming Style and a Complementary Software Tool",
Comput. Chem. Engng. 11, 45-61, 1987.
[6] A.K. Runchal, "Theory and application of the PORFLOW model for analysis
of coupled fluid flow, heat and radionuclide transport in porous media",
In: Coupled Processes Associated with Nuclear Waste Repositories,
Ed. C-F. Tsang, Academic Press, pp. 495-516, 1987
(see also http://acricfd.com/software/porflow/porpub.htm).
[7] F. King and M. Kolá![]() , "Prediction of the Lifetimes of
Copper Nuclear Waste Containers under Restrictive Mass-Transport and
Evolving Redox Conditions", CORROSION/95, paper No. 425,
NACE International, Houston, TX, 1995.
, "Prediction of the Lifetimes of
Copper Nuclear Waste Containers under Restrictive Mass-Transport and
Evolving Redox Conditions", CORROSION/95, paper No. 425,
NACE International, Houston, TX, 1995.
[8] F. King, M. Kolá![]() and D.W. Shoesmith, "Modelling the Effects
of Porous and Semi-Permeable Layers on Corrosion Processes",
CORROSION/96, paper No. 380, NACE International, Denver, Colorado, 1996.
and D.W. Shoesmith, "Modelling the Effects
of Porous and Semi-Permeable Layers on Corrosion Processes",
CORROSION/96, paper No. 380, NACE International, Denver, Colorado, 1996.
[9] M. Kolá![]() and F. King, "Modelling the consumption of oxygen by
container corrosion and reaction with Fe(II)",
In: Proc. of the XIXth Int. Symposium on Scientific Basis for
Nuclear Waste Management, Boston, Nov. 1995
(Mat. Res. Soc. Sym. Proc. 412, 547, 1996).
and F. King, "Modelling the consumption of oxygen by
container corrosion and reaction with Fe(II)",
In: Proc. of the XIXth Int. Symposium on Scientific Basis for
Nuclear Waste Management, Boston, Nov. 1995
(Mat. Res. Soc. Sym. Proc. 412, 547, 1996).
[10] F. King and M. Kolá![]() , "A numerical model for the corrosion
of copper nuclear waste containers", In: Proc. of the XIXth
Int. Symp. on Scientific Basis for
Nuclear Waste Management, Boston, Nov. 1995
(Mat. Res. Soc. Sym. Proc. 412, 555, 1996).
, "A numerical model for the corrosion
of copper nuclear waste containers", In: Proc. of the XIXth
Int. Symp. on Scientific Basis for
Nuclear Waste Management, Boston, Nov. 1995
(Mat. Res. Soc. Sym. Proc. 412, 555, 1996).
[11] F. King, M. Kolá![]() , S. Stroes-Gascoyne, P. Bellingham, J. Chu and
P.V. Dawe, "Modelling the Activity of Sulphate-Reducing Bacteria and the
Effects on Container Corrosion in an Underground Nuclear Waste Disposal
Vault", In: Proc. of the XXIIth Int. Symp. on the Scientific
Basis for Nuclear Waste Management, Fall 1998
(Mat. Res. Soc. Sym. Proc. 556, 1167, 1999).
, S. Stroes-Gascoyne, P. Bellingham, J. Chu and
P.V. Dawe, "Modelling the Activity of Sulphate-Reducing Bacteria and the
Effects on Container Corrosion in an Underground Nuclear Waste Disposal
Vault", In: Proc. of the XXIIth Int. Symp. on the Scientific
Basis for Nuclear Waste Management, Fall 1998
(Mat. Res. Soc. Sym. Proc. 556, 1167, 1999).
[12] F. King, M. Kolá![]() , and D.W. Shoesmith, "Modelling the oxidative
dissolution of UO2", In: Proc. of the XXIIth Int. Symp. on the
Scientific Basis for Nuclear Waste Management, Fall 1998
(Mat. Res. Soc. Sym. Proc. 556, 463, 1999).
, and D.W. Shoesmith, "Modelling the oxidative
dissolution of UO2", In: Proc. of the XXIIth Int. Symp. on the
Scientific Basis for Nuclear Waste Management, Fall 1998
(Mat. Res. Soc. Sym. Proc. 556, 463, 1999).
[13] F. King and M. Kolá![]() , "Mathematical implementation of the
mixed-potential model of fuel dissolution. Model Version MPM-V1.0",
Ontario Hydro Report, 06819-REP-01200-10005-R00, March 1999.
, "Mathematical implementation of the
mixed-potential model of fuel dissolution. Model Version MPM-V1.0",
Ontario Hydro Report, 06819-REP-01200-10005-R00, March 1999.
[14] F. King and M. Kolá![]() , "The copper container corrosion model
used in AECL's second case study", Ontario Power Generation Report,
06819-REP-01200-10041-R00, Sept. 2000.
, "The copper container corrosion model
used in AECL's second case study", Ontario Power Generation Report,
06819-REP-01200-10041-R00, Sept. 2000.
[15] M. Viscsek and T. Viscsek, "Intermittency, Stochastic Growth
and Phase Transition in a Simple Deterministic Partial Differential
Equation with a Singular Term", J. Phys. A: Math. Gen. 28,
L311-L316, 1995.
[16] G. Nicolis and I. Prigogine, "Self-Organization in Nonequilibrium
Systems", Wiley, New York, 1977.
[17] L.C. Harrison and M. Kolá![]() , "Coupling Between Reaction-Diffusion
Prepattern and Expressed Morphogenesis. ...", J. Theor. Biol.
130, 493-515, 1988.
, "Coupling Between Reaction-Diffusion
Prepattern and Expressed Morphogenesis. ...", J. Theor. Biol.
130, 493-515, 1988.
[18] A.M. Turing, Phil. Trans. R. Soc. Lond. B237, 37, 1952.
Appendix: TRANSIENT 4.3-beta "packing list"
A complete list (map) of all the files in all subdirectories of the
TRANSIENT 4.3-beta distribution package is in the HTML file index.html
which can be opened in a Web browser, and from which one can directly
inspect the contents of all the files.
| TRANSIENT "engine": | ||
| transien.c | The main, control, module. | |
| defs.h | TRANSIENT configuration file. | |
| transien.h |
|
|
| CTRLpar.h | List of control input parameters and their description. | |
| I/O functions: | ||
| InOut.c | File handling, input processing, output of control input parameters. | |
| transien.h | I/O for PDM-dependent input parameters. | |
| Auxiliary modules: | ||
| DateTime.c | A function returning the current date and time (to time-stamp the output files). | |
| DateLen.h | A header file for InOut.c and DateTime.c . | |
| incl_pri.h | Common #includes and printf macros. | |
| signals.c |
|
|
| NL3BANDV package: | ||
| nl3bandv.c | NL3BANDV solver for system of equation (8a). | |
| matrixv.c | Operations on linearly stored matrices. | |
| lufacv.c | LU factorization of linearly stored matrices. | |
| matinvv.c | Matrix inversion of linearly stored matrices. | |
| nl3band1.c |
|
|
| dynarr.c | Dynamical array allocation. | |
| nl3_ApBo.h | | These seven include files contain common code blocks for | |
| nl3_conv.h | | nl3bandv.c and nl3band1.c . | |
| nl3_Decl.h | | In particular, nl3_conv.h contains | |
| nl3_Rand.h | | the NR convergence criteria that | |
| nl3_runb.h | | can be customized by the user, | |
| nl3_strt.h | | if needed. | |
| nl3_Decl1.h | | | |
| Headers for NL3BANDV package: | ||
| matinvv.h | Used in nl3bandv.c . | |
| lufacv.h | Used in matinvv.c . | |
| dynarr.h |
|
|
| Makefiles: | ||
| makefile | UNIX makefile. | |
| makefile.VisualCpp | MC S Visual C++ makefile. | |
| OBJECTS | Microsoft C make file. | |
| MAKEDEMOS.COM | DCL command procedure for VMS. | |
| Documentation: | ||
| index.html | Web-browser entry point (map of the whole package in the HTML format). | |
| 00readme.txt | Main plain text readme file. | |
| doc/PDMtemplate.c | Template for PDM source files. | |
| doc/controls.txt | List, description, and default values of control input parameters. | |
| doc/function_lists.txt | List of all functions declared in all TRANSIENT's modules. | |
| doc/history.txt | TRANSIENT's history. | |
| doc/0license.txt | License agreement. | |
| doc/nl3_conv.h.V4.1 | For comparion: nl3_conv.h for version V4.1 | |
| doc/nl3_conv.h.V4.2 | And for the preceeding version V4.2 | |
| [doc/transien.tex] |
This manual. LATEX2e and LATEX2HTML ready.
Uses some color.
Sorry, transien.tex is currently missing from the V4.3-beta distribution archive. |
|
|
|
||
|
||
On Linux/UNIX, the case of the file names must be preserved (restored) as shown above.
These are file names used in the #include directives and the makefiles.
(When it is not done explicitly, throughout this Manual any reference to Unix
or Linux operating system should be understood as referring to both of them.)